2019~2020学年度上OI总结

CLJ 总结 哈希 Trie树 树状数组 分治 二分 三分 背包 树形DP 区间DP
创建时间:
阅读: 评论:

本文同步发表于$My luogu Blog$

从$CSP-J$后,差不多又有半年了,然后我们又要搞总结了~($≧▽≦)/~$


        

        




$1.$字符串$hash$
$       $简单来说,$Hash≈$把字符串转成$ULL.$
$       Q:$为什么要用$ULL?$
$       A:$利用$ULL$有自然溢出的特性，可以防止负数进而防止数组下标为负


$       $利用类似于进制的思想，我们就可以把一个字符串改造成$ULL$
cf2951ecbe045cf0949ea278e2c5437e_2_0_photo.png
而利用这个位值的原则，我们可以轻松地求出一个字符串中任意一个子串的值. 


$       $设:$p_i$表示在$base$进制下第$i$位的权值(事实上这可以用$base^{i-1}$轻松求得,但空间换时间大部分情况下是划算的),$h_i$表示$s_1-s_j$的子串$hash$值  


$       $所以可得:$s_l-s_r$的子串$hash$值为:  


其实感觉跟前缀和蛮像的  


这个原理很好证明，如果想不明白的话可以用十进制举例  


好像就没了?  


$2.$最小(大)表示法
$       $尽管$LF$没讲，但个人认为这还是很好理解的.
$       $以$P5990$为例,它要求一个字符串从顺时针，逆时针的顺序看过去的串是否有过，这其实相当于把这个字符串改成$12$个子串,我们求出这$12$个子串的$hash$值后取$min/max$即可表示与这个字符串等价的所有其他字符串.  


以样例为例:


1 2 3 4 5 6

它可以被改造为: 


1 2 3 4 5 6  
2 3 4 5 6 1
3 4 5 6 1 2
4 5 6 1 2 3
5 6 1 2 3 4
6 1 2 3 4 5

6 5 4 3 2 1  
5 4 3 2 1 6
4 3 2 1 6 5
3 2 1 6 5 4
2 1 6 5 4 3
1 6 5 4 3 2

这当中最小的应该是$\text{6 5 4 3 2 1}$这个子串的$hash$值，因此我们直接用$\text{6 5 4 3 2 1}$的值表示这$12$个串的值记录下来即可.  




个人认为这是学得仅次于$DP$烂的东西.  


$1.$概述
$       Q:$为什么要用字典树而不用字典链表什么的呢?




A:元素与元素间的关系为继承的一对多关系。




$       $拿字典树来说，每一个元素都可以有几个子元素，作为它之后的字母；而倘若要比对两个字符串是否相同，只需要比对在这棵字典树上，这两个串最后一个元素的祖先链(即前缀)是否相同，并且对于祖先链来说，并不用逐个比较，只需要记录访问就行  


$2.$怎么建一棵字典树?
$       $对于一棵字典树来说,我们用边来存储每一个字符?为什么呢?首先我们来想一想,字典树有没有根节点?  


$       $答案肯定是:”没有”,原因很简单,根节点的个数决定它树的棵树，如果根节点太多的话那这个数据结构没有方便可言.而且它叫字典树而不是字典森林  


$       $那没有根节点，也就没有了用点存储字符的可能性,因此用边是唯一的选择,节点的话，我们留着拿来编号用.  


int trie[N][26],End[N],tot=1;
void insert(char a[])
{
    int len=strlen(a),p=1;
    for(int i=0;i<len;i++)
    {
        int ch=a[i]-'a';
        if(trie[p][ch]==0)  trie[p][ch]=(++tot);
        p=trie[p][ch];
    }
    End[p]++;
}



$3.$查询
$        trie[i][ch]$表示$i$节点有$ch$这个字符,其编号为$tot$  


bool Search(char a[])
{
    int len=strlen(a),p=1,ans=0;
    for(int i=0;i<len;i++)
    {
        p=trie[p][a[i]-'a'];
        if (p==0) return false;
    }
    return true;
}



$       $这段代码表示查询前面有没有是它前缀的字符串.  


$       $那我们之前打的$End$标记是干吗的呢?我们把代码改成这个亚子.  


int Search(char a[])
{
    int len=strlen(a),p=1,ans=0;
    for(int i=0;i<len;i++)
    {
        p=trie[p][a[i]-'a'];
        if(p==0) return ans;
        ans+=End[p];
    }
    return ans;
}



$       $这就能查询之前建过的所有链中,有多少单词是当前要查询的单词的前缀 (好像还是没啥用?).  


$4.01 Trie$
$       01 Trie$树可以干吗?搞异或,求一个数列当中任意两个数异或能得到的最大值
$       $由异或的定义可得:   


$       $再根据一个小小的贪心，最高位如果是$1$的话,下面的低位不管是什么都比不上它的.
$       E.g:(1000)_2>(0111)_2$  


$       $所以剩下的就是，我们把一个数改成$32$位二进制数放在$Trie$树上，然后发现与当前位上不一样的数就直接往那条边走，否则就只能往当前位上和它相同数字方向走.  


$       $我能贴个$5996$的代码就跑吗?  




或许我有写过?  




$1.$二分
$       $对于一个有单调性的函数.(我们也可以把一个问题的解看做是一个单调函数)我们可以用二分求出它与$x$轴的交点(这个问题的解) 


$       $还是举个例子吧$P1314$ (好像这道题也可以三分?)
$       $对于这题，我们可以发现，选不同的$W$会有不同的差值,而$W$越大，矿石选的越少，$W$越小，矿石选的越多,自然,随着$W$增大,$Y$值减小
$       $所以我们需要做的,就只要二分$W$,然后对于每一个求出的$W$进行一次求解(要用前缀和优化)找到与目标$Y$最接近的值即可.  


$       $再举个例子$P2619$
$       $这道题我们可以清楚得看到，在保证最优解的情况下,选择白色边的数量是很难决定的.那不如……?我们先跑一边最优解(最小生成树),如果刚好有$need$条边,那么就可以直接输出,那如果不然呢? 


$       1.$如果它白边少了,那么我们可以让白边的权值$down$(减掉一个值),最后答案再$up$(加$need$条边回去)  


$       2.$如果它白边多了,那么我们可以让白边的权值$up$(加上一个值),最后答案再$down$(减$need$条边回去)  


$       $所以很明显,我们二分这个加/减去的值$(l-100,r=100)$,最后只要求得白边$\le need$即可更新答案.  


$2.$三分
$       $三分最常见的用法就是求一个区间单峰函数的极值,最常见的单峰函数是什么?当然就是二次函数啦~(≧▽≦)/~.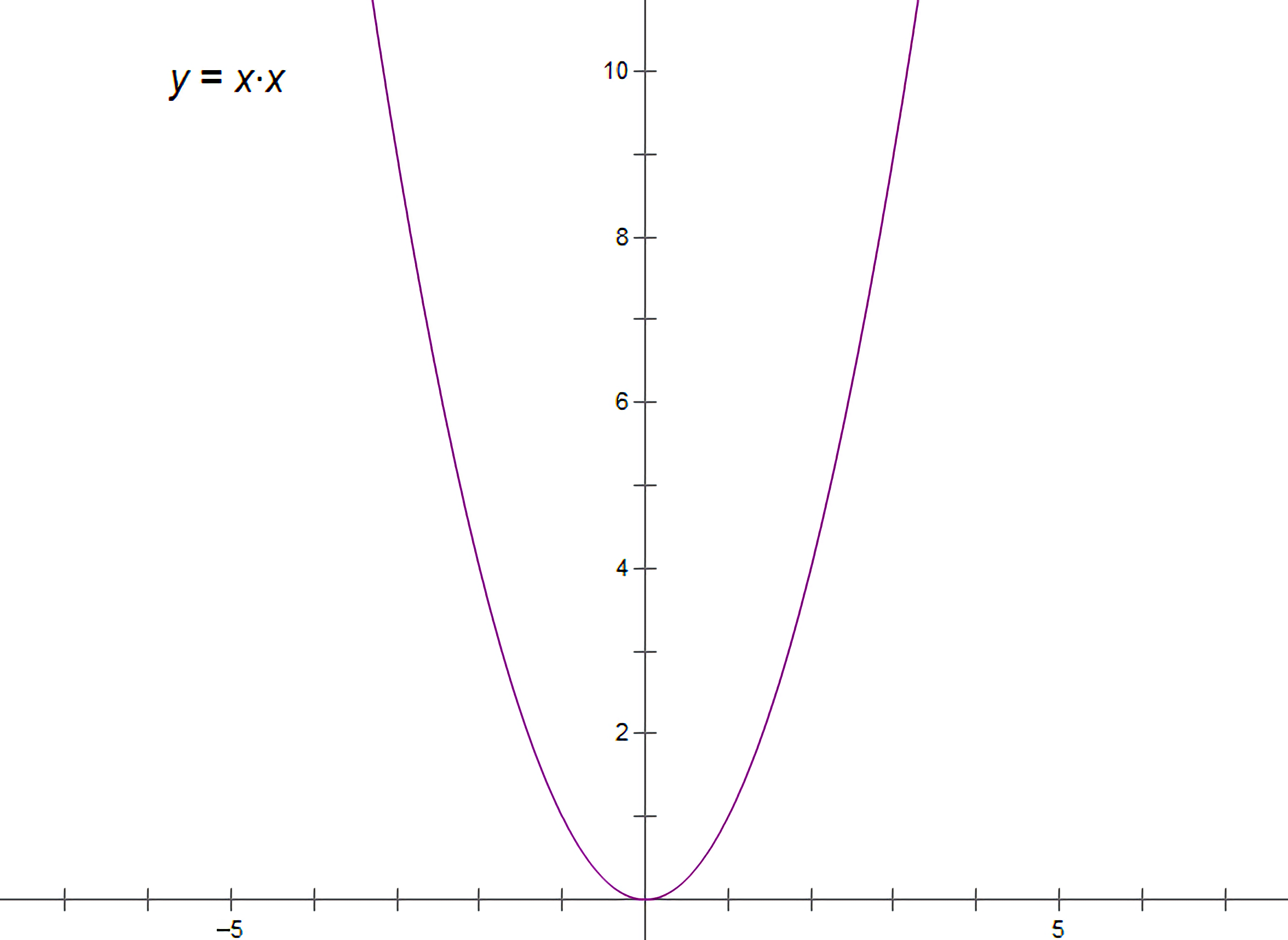
8f495fbf7a0ea76deb58e86555428b07_2_0_photo.png  


$       $对于一个二次函数，我们假设其定义域在$[l_i,r_i]$,我们手算的时候,假设这个区间为$[-3,3]$吧.  


$       $那么,我们可以求出这个区间的三等分点,对于这个例子来说,我们的三等分点就是$m1_x=l+\frac{r-l}{3}=1,m2_x=r-\frac{r-l}{3}=1$,它们的函数值相等,我们任意下移某一边的点,这里我们下移$l$，变为$[-1,3]$  


$       $继续计算,$m1_x=l+\frac{r-l}{3}=\frac{1}{3},m2_x=r-\frac{r-l}{3}=\frac{5}{3}$,$m1$的函数值小一些，我们把$l$下移下去.  


$       $它就会变成$[\frac{5}{3},3]$,以此类推,我们可以把$l$和$r$ 夹在一个范围之内.  


$       $了解了这些过后,我们就会明白$P3382$&$17$就是板子题了  


$3.EX$三分  




题目传送门:$OJ$$    $$Luogu$  




$      $先声明一下,我到现在都还是没有过掉,我不知道为什么它$WA$成$80$分,但我敢相信它的思路一定是正确的.  


$      $我们不难发现,总的时间一定是:  


$      $首先,我们可以假设传送带速度大于走路的速度,并且我们在$AB$段离开的点已经定下来为$E$点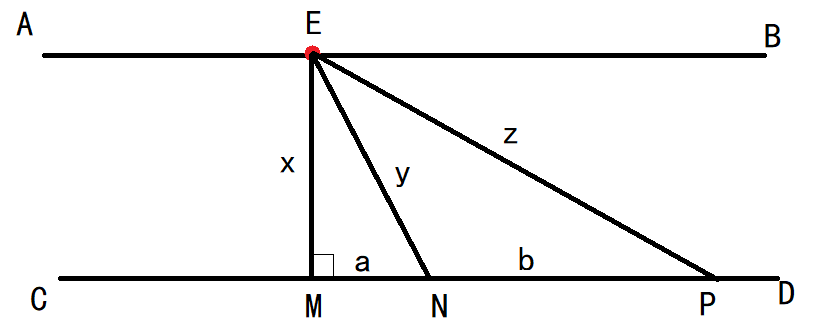
无标题.png
$      $我们假设$A→E→N→D$为最优路径,我们来看以下三种情况(讨论中我们自动忽略$A→E$与$P→D$的时间).  


$       $鉴于$x<y<z,$我们设$x=y-p,z=y+q$,所以我们的式子可以表示为:  


$       $将上述三个式子全都减掉相同的$\frac{y}{V}$,原式又会变为  


$       $一般情况下,$V_{CD}>V$,所以可以得到这是一个单峰函数的,当然,如果$V_{CD}<V$,那我们直接特判就好啦.  


$       $以此类推,我们也就得到了对于$AB$段的函数单峰性证明  (其实并没有,但我真的证不出来了)  


$       $所以这道题的正解就是,先三分$AB$上的$E$点,然后用三分出来的$E$点三分$CD$上的$F$点,然后用求得的最优解逼近最正确的$E$点.  




$       $码量过大,为防止卡顿故使用云剪贴板




$       $当然这道题也可以用模拟退火,粒子群优化和暴力(拆成$500$个点)乱搞  




$      $很明显,我有写过  




$      $我们会树,我们会$DP$,我们会树上$DP$.   


$1.$树的直径
$      $对于树的直径，我们普遍有两种做法


$      $一种是贪心两遍 $\text{dfs}$或 $\text{bfs}$,另外一种是树形 $\text{dp}$
$   $①.定义
$      $给定一棵树，
$      $树中每条边都有一个权值，
$      $树中两点之间的距离定义为连接两点的路径边权之和。
$      $树中最远的两个节点之间的距离被称为树的直径，
$      $连接这两点的路径被称为树的最长链
$      $简单来说，树的直径就是树上一条最长的链的距离  


$   $②.流程
$      $我们以下图为例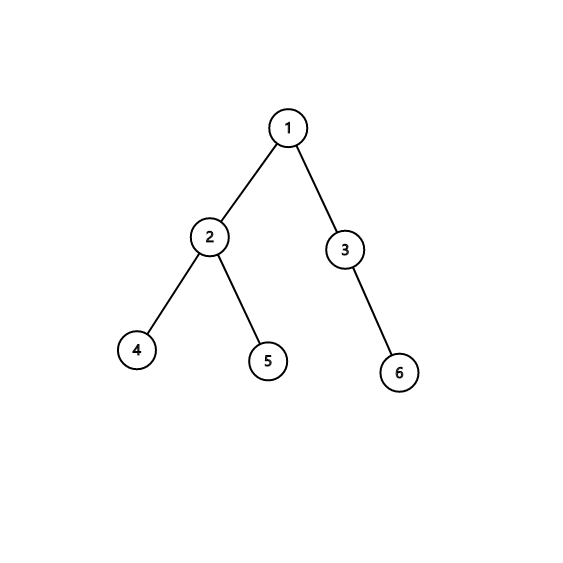
graph.png   


$      $我们任意选择一个点$W$,这里我们以$2$为例
$      $那么离$2$最远的就是$6$,我们再找一遍离$6$最远的节点:$4$。
$      $所以我们的最长链就是两次找到的两个节点所形成的链.
$      $至于正确性证明,可以看一下大佬的$\texttt{BLOG}$    


$      $而树形$\texttt{DP}$的话,我们可以用下面这种方法.   


$      $令$\texttt{DP1[i]}$表示起点为$i$的最长链,$\texttt{DP2[i]}$表示起点为$i$的(非严格)次长链,那么我们可以得到$ans=\max\{dp1[i],dp2[i]\}(1 \le i \le n)$
$      $所以转移方程肯定是这样写的($\text{u}$代表当前节点,$\text{v}$表示$\text{u}$的子节点):  


//当中的1全都可以换成w(边权)
if(dp1[u]<=dp1[v]+1)
{
    dp2[u]=dp1[u];//这两个顺序不能变换
    dp1[u]=dp1[v]+1;
}
else if(dp2[u]<=dp1[v]+1) dp2[u]=dp1[v]+1;//else 不能去掉



$       $这个意思应该很清楚吧,如果我们能更新最长链,那么我们先更新次长链为当前最长链,最长链为当前新得到的值.
$       $如果上面这个不成立,我们再来找一下能不能更新次长链
$       $所以很明显,找直径的树形$\text{DP}$是由子节点到根节点的.
$       $例题传送门:$160$
$       $乍一看这道题都跟树没有关系,然而事实上,我们可以把可以互相转化的数看做是在这两个节点之间连了一条边,因此这道题就是求一个树上的最长链,即树的直径.


$       $由于这道题一定是从大数转换为小数,所以我们倒序枚举即可.  


#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int sum[50005],d1[50005],d2[50005];
int main() {
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        for(int j=2;j<=n/i;j++) sum[i*j]+=i;
    }
    for(int i=n;i>=1;i--)
    {
        if(sum[i]<i)
        {
            if(d1[i]+1>d1[sum[i]])
            {
                d2[sum[i]]=d1[sum[i]];
                d1[sum[i]]=d1[i]+1;
            }
            else if(d1[i]+1>d2[sum[i]]) d2[sum[i]]=d1[i]+1;
        }
    }
    int ans=-1;
    for(int i=1;i<=n;i++) ans=max(ans,d1[i]+d2[i]);
    printf("%d",ans);
    return 0;
}



$2.$树的最大独立集
$       $这个,怎么说呢?其实就是给定一些限制,然后在满足这些限制的前提下最多/最少能取多少个点.
$       $具体我们以找一道例题把.
$       $解析在这里.  


$3.$树的重心
$       $考虑一个点，以它为根的树中，最大的子树节点数最少，我们把这个点称为树的重心
$       $举个例子，下图中重心为 $1$ 和 $2$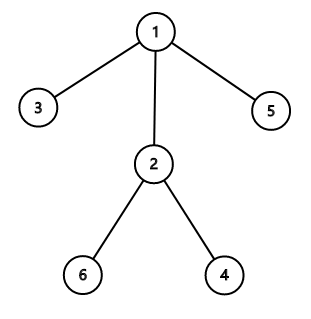
graph.png
$   $①求法
$       $求解树的重心的时候，我们通常会采用树形 $\text{dp}$
$       $我们用 $s[i]$ 代表以 $i$ 为根的子树节点数
$       dp[i]$代表以 $i$ 为根的子树中最大的子树节点个数
$       $显然，$dp[u]=\max(dp[u],s[v])$
$       $但是我们求重心的时候，是以 $u$ 为根。
$       $还是举上图的例子，当我们把$2$号点当成重心时，它就变成了这样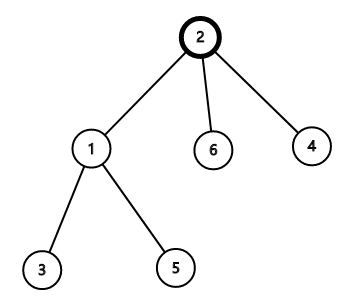
graph _1_.png
$       $这时候 2 号节点的父亲变成了儿子
$       $所以最后统计 $dp[u]$ 的时候，还要记得统计 $n-s[u]$(即以原来父亲为根的子树的节点数)  


$       $还是搞一个例题吧.
$       $题目传送门:$OJ$$   $$SP9942$
$       $我想知道为什么我考场上没有看出来这是重心  


$       $我们求出来以原来每一个点的父亲一坨子树还是儿子一坨子树的节点数多,那么我们就让多的经过这条边即可.  




$       $$Here it is!$  




$       $树形$DP$先讲三大模板吧,后面再填坑.  




To Be Continued






$    1.$模板?
$        $区间$\text{DP}$一般有这样的套路.  


for(int len=2;len<=n;len++)
{
    for(int i=1;j=len;j<=n;i++,j++)
    {
        for(int k=i;k<j;k++)
        {
            dp[i][j]= (max or min) (dp[i][j],dp[i][k] (+ or *) dp[k+1][j] (+ or *) (视题目而定) )
        }
    }
}



$    $2.套路
$        $ 区间$\text{DP}一般有一个$
$        $ 破环为链 $  \Theta(n)$ ,代码简单,不展示了.
$        E.g$:$1552$$    $$P1880$  


$    $3.例题  




$        $$OJ$$   $  $Luogu$  




$         $我们记$\text{op[i]}$表示第$\text{i}$条边的操作,设$\text{dp[i][j]}$表示在$i-j$的边序列操作后所能得到的最大值.
$         $我们很容易就能发现:  


$         $于是你高高兴兴地交上去,发现只有$80pts$  


$         $为什么呢? 这可是IOI诶,即使再水也不至于这样吧. 我们来看一下数据范围  




$         $顶点数字都在$[-32768,32767]$ 




$         $所以很明显,这里是因为负数$\times$负数很有可能超过当前最大值,所以我们还要维护一个最小值。  


$         $设:$\texttt{DP1[i][j]}$维护最小值,$\texttt{DP2[i][j]}$维护最大值
$         $那么我们的状态转移方程就会变成下面这个亚子.  


$        $乘法完整打出来有$8$行,所以我稍微简化了一下,$dp1/2[i][j]$表示它既得取$dp1$,又得取$dp2$.  




Here it is!






      
       
 转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 1275881998@qq.com 
    








    
文章标题:2019~2020学年度上OI总结

    
    
本文作者:Forgotten

    
发布时间:2020-01-30, 21:45:00

    
最后更新:2020-02-14, 22:43:33

    原始链接:http://forgotten-myself.github.io/2020/01/30/2019~2020%E5%AD%A6%E5%B9%B4%E5%BA%A6%E4%B8%8AOI%E6%80%BB%E7%BB%93/
    

        版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。
    






    








    
        







    




    

    

        
©2017 Forgotten


Built with Hexo and 3-hexo theme


    

    

        


目录