DP 100题
- DP100 目录和前言
- 动态规划100题 1~10 题
- 动态规划100题 11~20 题
- 11.「CF1101D」GCD Counting(思维树形 dp)
- 12.「JSOI2018」潜入行动(不简单的背包树形 dp)
- 13.「CF1114D」Flood Fill(套路区间 dp)
- 14.「CF149D」Coloring Brackets(限制性区间 dp)
- 15.「CQOI2009」叶子的染色(猜结论+树形 dp)
- 16.「HAOI2016」字符合并(区间 dp x 状压 dp)
- 17.「GXOI/GZOI2019」宝牌一大堆(我也不知道是什么 dp)
- 18.「UVA1452」Jump(约瑟夫问题变形)
- 19.「CF235B」Let’s play OSU! 和 「BZOJ4318」OSU!(期望 dp)
- 20.「CF76F」Tourist(LIS 变形)
DP100 目录和前言
前言
$ $其实我也不知道为什么要开这么一个坑。
$ $CSP 已经结束了,又是新的一年。本着 dp 不好的原则,想练一下 dp,通过这个坑,不仅锻炼自己的 dp 水平,还能提高写博客的技巧,何乐而不为呢?
$ $2019/12/17 这个日子,晚自习的时候突然脑子一抽想来开这么一个坑。想法告诉了巨佬wy,lyc,xc,zyz以及tr之后得到了鄙视以及一句你疯了大力支持,再次膜拜。
$ $本着鸽子的精神,我争取在半年之内开到100题,也希望不会咕咕吧。。。
$ $最后题目不会太水,由易到难(稍微考虑了一下,第一道就蓝了不至于吧,第六道就紫了也不至于吧。。。随便找点紫的黑的做着玩就行啦qwq),希望能够加强自己的 dp 水平吧。
$ $附加,如果没用正解弄过去(比如打表,搜索,O2等等),如果不是的确可以很正常的想到优化的话,请不要像小学生一样盖楼。谢谢。
半年怕是结不了束了
$ $当前进度 20/100
Attention!
$ $考虑加载实在是太慢,分析之后认为,我们需要分开成 10 份,每份 10 道题(不然会卡死xd),大概只会贴一个 Link 了。
Index
$ $1~10 题
$ $11~20 题
「NOI2001」炮兵阵地(简单状压 dp)
「JSOI2016」病毒感染(dp 预处理拆开复杂度处理)
「ZJOI2007」棋盘制作(dp + 单调栈经典模型)
「SEERC2019」Game on a Tree(博弈论类树形 dp)
「NOI1997」积木游戏(较难的线性 dp)
「HAOI2006」数字序列(很牛逼的线性 dp + 数学证明)
「GZOI2017」取石子游戏(博弈论类 dp)
「SCOI2005」最大子矩阵(简单 dp)
「SNOI2017」英雄联盟(背包 dp)
「HAOI2015」树上染色(树形类背包 dp)
「CF1101D」GCD Counting(思维树形 dp)
「JSOI2018」潜入行动(不简单的背包树形 dp)
「CF1114D」Flood Fill(套路区间 dp)
「CF149D」Coloring Brackets(限制性区间 dp)
「CQOI2009」叶子的染色(猜结论+树形 dp)
「HAOI2016」字符合并(区间 dp x 状压 dp)
「GXOI/GZOI2019」宝牌一大堆(我也不知道是什么 dp)
「UVA1452」Jump(约瑟夫问题变形)
「CF235B」Let’s play OSU! 和 「BZOJ4318」OSU!(期望 dp)
「CF76F」Tourist(LIS 变形)
动态规划100题 1~10 题
1.「NOI2001」炮兵阵地(简单状压 dp)
$ $luogu
$ $首先观察题目,我们发现不能用传统的方式去定义我们的 dp 数组,因为 $dp_{i,j}$ 甚至维度更高似乎无法有效地储存状态。并且我们的影响范围还会影响到前两行,怎么办呢?
$ $我们发现 $n,m$ 都是很小的,炮兵影响范围相对来说也是比较小的。我们考虑状压 dp。首先我们定义一行炮兵排列合法,当且仅当炮兵互相之间不冲突,并且炮兵不会放置在山上。于是我们考虑在 dp 数组之间带上前 1 行的状态和当前行状态。为什么不考虑前两行呢?是因为我们转移的时候,确定前 1 行合法,那么前 2 行会被当做前 1 行的前 1 行处理掉。
$ $我们考虑如何保存状态。我们将状态压缩成一个数 $S$。这个 $S$ 转化成二进制,如果第 $x$ 位是 1,就代表第 $x$ 位有炮兵。
$ $根据上面,我们可以很自然地定义出 $dp_{i,S,T}$ 为第 $i$ 行状态为 $S$,$i-1$ 行状态为 $T$ 的放置最多炮兵数。有 dp 方程:
$ $其中 $i,S,T$ 如上定义,$U$ 即为 $i-2$ 行的状态。其中满足:
$S \& T=0$。
$S \& U=0$。
$T \& U=0$。
$S,T,U$ 都合法。
$3 \leq i \leq n$.
$ $有了这些,很容易得到我们的答案即为 $\sum dp_i,S,T$。其中 $i,S,T$ 需要枚举计算答案。
$ $同时,我们需要预处理。我们从第 1 行开始。如果这一行选择状态 $K$ 是可以的,那么我们的 $dp_{1,K,0}=|K|$,其中 $|K|$ 为 $K$ 转化成二进制之后有多少个 1。计算这个东西有两种方法:
int __builtin_popcount(int x);
long long __builtin_popcountll(long long x);
$ $内置函数,可直接使用,但是很慢。。。最好别用。
int lowbit(int x){return x&(-x);}
int popcount(int x)
{
int ans=0;
while(x)
{
x-=lowbit(x);
++ans;
}
return ans;
}
$ $预处理 $dp_2$ 也是很简单的,仍然是枚举计算。
$ $我们的时间复杂度 $O(n \times 2^{3m})$。但实际上加上我们不合法序列的剪枝,跑的会快很多。但是这道题卡空间。。。
$ $我们发现我们的状态只跟前两行有关,于是我们可以把第一位滚掉,就不会 MLE 了。
#include<cstdio>
#include<algorithm>
#define BuiPop(i) __builtin_popcount(i)
#define last j
#define now k
#define lastslast l
using namespace std;
int dp[3][1025][1025],a[105],n,m,ans;
char c[15];
void Prepare()
{
for(int i=0;i<(1<<m);++i) if(!(i&(i<<1) || i&(i<<2) || i&a[1])) dp[1][i][0]=BuiPop(i);
for(int i=0;i<(1<<m);++i) for(int j=0;j<(1<<m);++j) if(!(i&j || i&(i<<1) || i&(i<<2) || j&(j<<1) || j&(j<<2) || i&a[1] || j&a[2])) dp[2][j][i]=BuiPop(i)+BuiPop(j);
}
void DynamicProgramming()
{
for(int i=3;i<=n;++i)
{
for(int j=0;j<(1<<m);++j)//last
{
if(j&(j<<1) || j&(j<<2) || j&a[i-1]) continue;
for(int k=0;k<(1<<m);++k)//now
{
if(j&k || k&(k<<1) || k&(k<<2) || k&a[i]) continue;
for(int l=0;l<(1<<m);++l)//last's last
{
if(l&j || l&k || l&(l<<1) || l&(l<<2) || l&a[i-2]) continue;
dp[i%3][now][last]=max(dp[i%3][now][last],dp[(i-1)%3][last][lastslast]+BuiPop(k));
}
}
}
}
}
void GetAnswers()
{
for(int i=0;i<(1<<m);++i) for(int j=0;j<(1<<m);++j) ans=max(ans,dp[n%3][i][j]);
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i)
{
scanf("%s",c+1);
for(int j=1;j<=m;++j)
{
a[i]<<=1;
if(c[j]=='H') a[i]|=1;
}
}
Prepare();
DynamicProgramming();
GetAnswers();
printf("%d",ans);
return 0;
}
2.「JSOI2016」病毒感染(dp 预处理拆开复杂度处理)
$ $luogu
$ $算是一道简单的 dp 题了。
$ $我们直接暴力 dp 会发现 $O(n^3)$ 的时间复杂度只能得 $50\%$ 的分,于是我们考虑优化。
$ $瓶颈在于我们无法快速计算 $i → j → i$ 途中的最少死亡的人数。于是我们把两样东西拆开来进行计算。
$ $因为村庄排成一条链,我们定义 $sum_i=\sum_{j=1}^i a_j$。
$ $我们定义 $dp_{i,j}$ 为 $i → j → i$ 途中的最少死亡的人数,枚举 $i$ 为起点, $j$ 为长度,可以得到这个 dp 方程:
$ $至此,我们用 $O(n^2)$ 的时间复杂度完成了预处理,接下来就是计算答案。
$ $我们定义 $dp2_i$ 为当前在村庄 $i$ 并且 $i$ 到 $i$ 以前的村庄疫情消灭的总消失最小人数,我们可以快速得到:
$ $至此,时间复杂度 $O(n^2)$,可以解决问题。
#include<cstdio>
#include<cstring>
long long min(long long x,long long y){return x<y?x:y;}
long long n,dp[3005][3005],dp2[3005],sum[3005],a[3005];
int main(){
scanf("%lld",&n);
for(long long i=1;i<=n;++i) scanf("%lld",&a[i]),sum[i]=sum[i-1]+a[i];
for(long long i=1;i<=n-1;++i) for(long long j=1;j<=n-i;++j) dp[j][i+j]=dp[j+1][i+j]+min((sum[i+j]-sum[j])*2,a[j]*i*3+sum[i+j]-sum[j]);
memset(dp2,0x3f,sizeof dp2);//设置极大值
dp2[0]=0;
for(long long i=1;i<=n;++i) for(long long j=0;j<i;++j) dp2[i]=min(dp2[i],dp2[j]+dp[j+1][i]+(4*i-4*j-2)*(sum[n]-sum[i]));
printf("%lld",dp2[n]);
return 0;
}
3.「ZJOI2007」棋盘制作(dp + 单调栈经典模型)
$ $luogu
$ $我们要找到一个黑白相间的棋盘(可以参考国际象棋棋盘),第一个小问题是找到最大的正方形,第二个是找到最大的矩形。
$ $我们注意到棋盘跟题 1 一样只有两种格子,能用状压吗?答案是否。因为 $n,m \leq 2000$,所以不能状压。
$ $同时,找到最大的合法正方形和矩形,恰好是我们的找纯色最大正方形和矩形的经典模型(分别用 dp 和单调栈求解),我们能够在此间转换吗?
$ $答案是可以的。我们将 $a_{i,j} \oplus 1 (i + j \mod 2 = 0)$,其中 $\oplus$ 为异或符号。
$ $我们发现随机取上一个矩阵,我们翻转了之后,发现其实就是可以互相转换的。现在我们反转之后只需要求纯色最大正方形和矩形的经典模型了。
$ $对于第一个问题,定义 $dp_{0,i,j}$ 为 $a_{i,j}=0$,以 $(i,j)$ 为右下角的正方形最大边长。$dp_1$ 同理。对于 dp 方程,有:
$ $易得答案为 $\max \{ dp \}$,时间复杂度 $O(nm)$。
$ $对于第二个问题,用单调栈求解。我们首先储存一段连续的高,也就是对于一个数最多能往上延伸多少相同的连续的数。枚举每一行作为矩形底边,这道题就变成了直方图最大矩形问题。枚举下边时间复杂度 $O(n)$,单调栈 $O(m)$。
$ $得到这些,总时间复杂度 $O(nm)$,可以通过题目。感谢 S-LJS 搬运到校OJ。公开之后会发链接。
$ $代码如下。
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int n,m,a[2005][2005];
namespace DynamicProgramming
{
int dp1[2005][2005],dp2[2005][2005];
void Dp()
{
int ans=0;
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
if(a[i][j]) dp1[i][j]=min(min(dp1[i-1][j],dp1[i][j-1]),dp1[i-1][j-1])+1;
else dp2[i][j]=min(min(dp2[i-1][j],dp2[i][j-1]),dp2[i-1][j-1])+1;
ans=max(ans,max(dp1[i][j],dp2[i][j]));
}
}
printf("%d\n",ans*ans);
}
}
namespace MonotonicStack
{
int cnt[2005][2005],ans,s[2005],l[2005];
void Monotonic(int sp[])
{
int top=0,len=0;
s[top]=l[top]=0;
for(int i=1;i<=m;++i)
{
if(sp[i]>=s[top]) s[++top]=sp[i],l[top]=1;
else
{
len=0;
while(top && s[top]>sp[i])
{
len+=l[top];
ans=max(ans,len*s[top]);
--top;
}
s[++top]=sp[i];
l[top]=len+1;
}
}
len=0;
while(top)
{
len+=l[top];
ans=max(ans,len*s[top]);
--top;
}
}
void Stack(){for(int i=1;i<=n;++i) Monotonic(cnt[i]);}
void Ans(){printf("%d",ans);}
}
using namespace MonotonicStack;
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
scanf("%d",&a[i][j]);
if(!((i+j)&1)) a[i][j]^=1;
if(a[i][j]) cnt[i][j]=cnt[i-1][j]+1;
}
}
DynamicProgramming::Dp();
MonotonicStack::Stack();
memset(cnt,0,sizeof cnt);
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
if(!a[i][j]) cnt[i][j]=cnt[i-1][j]+1;
}
}
MonotonicStack::Stack();
MonotonicStack::Ans();
return 0;
}
4.「SEERC2019」Game on a Tree(博弈论类树形 dp)
$ $luogu
$ $题意转化:有一棵以 1 为根的树,每个节点的初始颜色为白色。Alice 先让任意一个节点放上标记变黑作为一次操作。然后 Bob 开始,轮流移动这个标记到当前所在节点的任意一个白色的祖先或者后代节点,并且把它这个节点染成黑色。谁不能移动谁就输了。
$ $考虑这个树上博弈问题。首先引进树的最大匹配。不会的同学,可以自查博客。
$ $首先假设我们只能够走到相邻的节点,我们发现我们只需要判断这棵树是否满足,它的最大匹配是一个完美匹配。如果是的话,后手必胜,否则先手一定能够避免,于是先手必胜。
$ $回到问题,我们不只是走到相邻的节点。但是思路相同,这个问题我们用树形 dp 求解。
$ $定义 $dp_i$ 为节点 $i$ 以及该节点对应子树未匹配节点的最小数量,$cnt=\sum_{\texttt{以i为根节点的后代j}} dp_j$
$ $如果 $dp_1=0$ ,则说明先手必胜。
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
vector<int> G[100005];
int dp[100005],n;
bool vis[100005];
void dfs(int now,int pre)
{
bool flag=false;
for(unsigned int i=0;i<G[now].size();++i)
{
if(G[now][i]==pre) continue;
dfs(G[now][i],now);
flag|=vis[G[now][i]];
dp[now]+=max(dp[G[now][i]],vis[G[now][i]]?1:0);
}
if(!flag || dp[now]>0) vis[now]=true;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n-1;++i)
{
int x,y;
scanf("%d %d",&x,&y);
G[x].push_back(y);
G[y].push_back(x);
}
memset(dp,-1,sizeof dp);
dfs(1,0);
puts(dp[1]?"Alice":"Bob");
return 0;
}
5.「NOI1997」积木游戏(较难的线性 dp)
$ $luogu
$ $我们定义 $dp_{i,j,k}$ 为前 $i$ 个积木垒成 $j$ 堆,并且当前正在处理第 $k$ 个平面。$0 \leq k \leq 2$,分别代表积木不同的三面。
$ $我们很容易发现我们可以再多垒成一堆,也可以搭在当前这一堆积木上面。但是一定要注意再新垒成一堆的话就不用判断之前的积木的长宽高了。
$ $我们能够很顺利地推出我们的转移方程:
$ $如果还可以垒到当前的积木上面去:
$ $其中 $i,j$ 意义如上,$k$ 为当前选到要搭上的积木,$pm$ 为当前平面,$Last$ 为上个平面。
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<queue>
using namespace std;
int n,m,a[105],b[105],c[105],dp[105][105][3];//dp[i][j][k]:前i个堆垒j个正在处理k平面
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i) scanf("%d %d %d",&a[i],&b[i],&c[i]);//进行输入
for(int i=1;i<=m;++i)
{
for(int j=1;j<=n;++j)
{
for(int k=0;k<j;++k)
{
for(int pm=0;pm<=2;++pm)
{
int x,y,buf;
if(pm==0) x=a[j],y=b[j],buf=c[j];
if(pm==1) x=b[j],y=c[j],buf=a[j];
if(pm==2) x=c[j],y=a[j],buf=b[j];
if(x<y) x^=y^=x^=y;
for(int Last=0;Last<=2;++Last)
{
int xx,yy;
if(Last==0) xx=a[k],yy=b[k];
if(Last==1) xx=b[k],yy=c[k];
if(Last==2) xx=c[k],yy=a[k];
if(xx<yy) xx^=yy^=xx^=yy;
dp[i][j][pm]=max(dp[i][j][pm],dp[i-1][k][Last]+buf);
if(x>xx || y>yy) continue;
dp[i][j][pm]=max(dp[i][j][pm],dp[i][k][Last]+buf);
}
}
}
}
}
int ans=-10086001;
for(int i=1;i<=n;++i) ans=max(ans,max(max(dp[m][i][0],dp[m][i][1]),dp[m][i][2]));
printf("%d",ans);
return 0;
}
6.「HAOI2006」数字序列(很牛逼的线性 dp + 数学证明)
$ $luogu
$ $dp 一步走,简化题意。也就是说改变一个序列里面的某些元素使得序列严格单调上升,并且修改元素最少。在满足上一个情况下,我们改变元素的幅度最小,也就是 $\sum _{i=1} ^n |a_i-fix_i|$ 最小。
$ $但是我们如何确定修改元素最少呢?似乎没有很显然的方法。于是我们考虑使不修改元素尽量多,也就可以让我们有 dp 思路。
$ $两个元素不修改的必要条件,当且仅当 $a_i,a_j(1 \leq i \le j \leq n)$,满足 $a_i+j-i \leq a_j$。转化之后得到 $a_i-i \leq a_j-j$。我们将所有的 $a_i-i$,第一个小问题就转化成了当前 $a$ 序列的 $LIS$。注意用 $O(n \log n)$ 的方法去转化。这里得到的 dp 值下文记为 $f_i$。
$ $考虑第二个子问题。我们定义 $dp_i$ 为修改 1~i 使 $a$ 严格单调上升的最小代价。有 $cost_{j,i}$ 为把区间 $[j,i]$ 严格单调上升的最小代价,自然得到 dp 方程:
$ $因为有 $dp_j+1=dp_i$,可以有 $cost_{j,i}$ 的决策中,$\forall k → [j,k]$ 所有元素为 $a_j$ 并且 $[k+1,l]$ 的元素都为 $a_i$。
$ $有了猜想,如何证明结论成立?
偷了张图,可以自己体会一下。
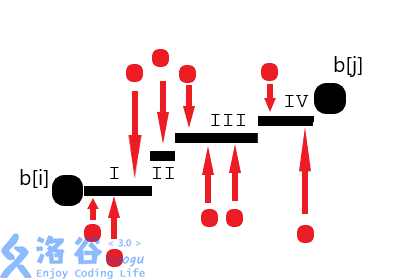
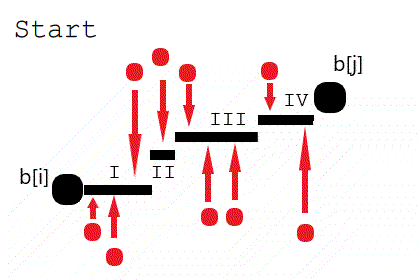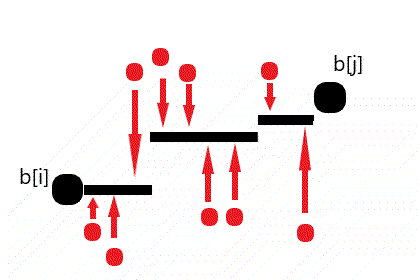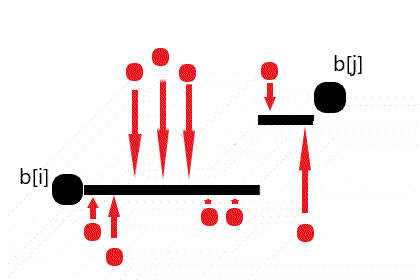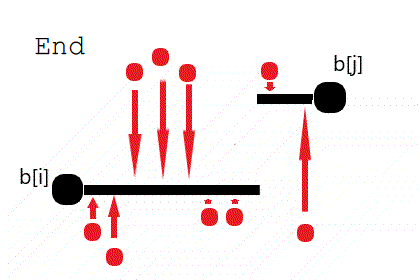
$ $偷懒就不证明了吧。。。反正 luogu 上面证明多得是。
$ $有了这些,实际上我们遇到这样的值就进行 dp。最坏复杂度 $O(n^3)$。但是因为我们的数据随机,所以怎么 dp 都不死。xd
$ $代码如下。
#include<cstdio>
#include<algorithm>
#include<queue>
#define inf 1008600110086001ll
using namespace std;
vector<long long> G[35005];
long long a[35005],n;
long long Abs(long long x){return x<0?-x:x;}
namespace Subtasks{
long long dp[35005],seq[35005],sum1[35005],sum2[35005],ddpp[35005];
void Subtask1()
{
a[++n]=inf;
long long len=1;
seq[1]=a[1],dp[1]=1;
for(long long i=2;i<=n;++i)
{
if(a[i]>=seq[len]) seq[++len]=a[i],dp[i]=len;
else
{
long long whe=upper_bound(seq+1,seq+1+len,a[i])-seq;
seq[whe]=a[i],dp[i]=whe;
}
}
printf("%lld\n",n-len);
}
void prepareForSubtask2()
{
for(long long i=0;i<=n;++i) G[dp[i]].emplace_back(i),ddpp[i]=inf;
ddpp[0]=0;
a[0]=-inf;
}
void Subtask2()
{
for(long long i=1;i<=n;++i)
{
for(unsigned long long j=0;j<G[dp[i]-1].size();++j)
{
long long to=G[dp[i]-1][j];
if(a[to]<=a[i])
{
sum1[to-1]=sum2[to-1]=0;
for(long long k=to;k<=i;++k) sum1[k]=Abs(a[k]-a[to])+sum1[k-1],sum2[k]=Abs(a[i]-a[k])+sum2[k-1];
for(long long k=to;k<=i;++k) ddpp[i]=min(ddpp[i],ddpp[to]+sum1[k]-sum1[to]+sum2[i]-sum2[k]);
}
}
}
printf("%lld\n",ddpp[n]);
}
}
int main(){
scanf("%lld",&n);
for(long long i=1;i<=n;++i) scanf("%lld",&a[i]),a[i]-=i;
Subtasks::Subtask1();
Subtasks::prepareForSubtask2();
Subtasks::Subtask2();
return 0;
}
7.「GZOI2017」取石子游戏(博弈论类 dp)
$ $luogu
$ $我们因为不知道第一堆石子到底是哪一堆,所以说我们直接枚举。
$ $我们考虑让 Bob 后手赢这场游戏,所以说 Alice 在一开始或者第二回合变成必败状。做了nim游戏的板子的都知道必败状是 $a_1 \oplus a_2 \oplus … \oplus a_n=0$($\oplus$ 为异或符号),我们要让 Alice 面对必败状,我们只能让剩下的 $n-1$ 堆石子异或起来大于等于第一堆。因为如果小于的话,Alice 一定能找到一种方法取第一堆石子使得 $a_1 \oplus a_2 \oplus … \oplus a_n=0$。
$ $同时,我们发现 $a_i$ 极其之小,异或起来最多也不过 $2^8-1=255$,我们考虑把它作为dp数组的一维。
$ $那么我们定义 $dp_{i,j}$ 为前 $i$ 堆除了枚举的第 $k$ 堆外异或起来的数为 $j$ 的方案,然后每次跑一边 dp,统计一遍答案即可。
$ $时间复杂度 $O(n^2 \log a_i)$,其中 $\log a_i$ 最大为 $8$,近似于常数。
$ $代码如下。
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#define MOD 1000000007ll
using namespace std;
long long n,a[205],dp[205][260],ans;
int main(){
scanf("%lld",&n);
dp[0][0]=1;
for(long long i=1;i<=n;++i) scanf("%lld",&a[i]);
for(long long i=1;i<=n;++i)
{
for(long long j=1;j<=n;++j)
{
for(long long k=0;k<=255;++k)
{
if(i==j) dp[j][k]=dp[j-1][k];//这里一定要跳过,去掉我们枚举的“第一堆”
else dp[j][k]=dp[j-1][k]+dp[j-1][k^a[j]],dp[j][k]%=MOD;
}
}
for(long long j=a[i];j<=255;++j) ans+=dp[n][j],ans%=MOD;//统计第i堆作为第1堆的答案
}
printf("%lld",ans);
return 0;
}
8.「SCOI2005」最大子矩阵(简单 dp)
$ $luogu
$ $初看题目,$m \leq 2$。很容易发现我们经常做这种开两个算法去做的题。于是分析题目,觉得应该是可以的。
$ $对于这种题,我们发现 $m = 1$ 的时候,就是我们的的经典模型:在 $n$ 个数中选 $k$ 个不相连的子串。我们可以定义 $dp_{i,j,0/1}$ 为第 $i$ 个选到第 $j$ 个子序列,对于 $a_i$ 选与不选两种情况。得到 dp 式:
$ $答案即为 $\max \{dp_{n,k,0},dp_{n,k,1}\}$。
$ $有了我们在 $m=1$ 的成功经验,为什么不去试试 $m=2$ 呢。
$ $可见 $m=2$ 时只有 5 种情况。分别是:
空出一行;
选择左边而空出右边;
选择右边而空出左边;
左边和右边分别属于两个矩阵;
左右属于一个矩阵。
$ $然后根据这些东西,我们一样可以像上面一样得到转移方程,可惜这里太小写不下。(XD其实是太长了)
$ $看看代码就行了。
#include<bits/stdc++.h>
using namespace std;
int n,m,k;
namespace std
{
namespace Subtask1
{
int dp[105][15][2];
int Solve()
{
for(int i=1;i<=n;++i)
{
int x;
scanf("%d",&x);
for(int j=1;j<=k;++j)
{
dp[i][j][1]=max(dp[i-1][j][1]+x,dp[i-1][j-1][0]+x);
dp[i][j][0]=max(dp[i-1][j][1],dp[i-1][j][0]);
}
}
return 0&printf("%d",max(dp[n][k][1],dp[n][k][0]));
}
}
namespace Subtask2
{
int dp[105][15][5];
int Solve()
{
memset(dp,-0x3f,sizeof dp);
for(int i=0;i<=n;++i) for(int j=0;j<=k;++j) dp[i][j][0]=0;
for(int i=1;i<=n;++i)
{
int a,b;
scanf("%d %d",&a,&b);
for(int j=1;j<=k;++j) dp[i][j][0]=max({dp[i-1][j][0],dp[i-1][j][1],dp[i-1][j][2],dp[i][j-1][3],dp[i-1][j][4]}),dp[i][j][1]=max({dp[i-1][j-1][0],dp[i-1][j][1],dp[i-1][j-1][2],dp[i-1][j][3],dp[i-1][j-1][4]})+a,dp[i][j][2]=max({dp[i-1][j-1][0],dp[i-1][j-1][1],dp[i-1][j][2],dp[i-1][j][3],dp[i-1][j-1][4]})+b,dp[i][j][3]=max({dp[i-1][j-1][1],dp[i-1][j-1][2],dp[i-1][j][3],(j>=2?dp[i-1][j-2][4]:-2147483647)})+a+b,dp[i][j][4]=max({dp[i-1][j-1][0],dp[i-1][j-1][1],dp[i-1][j-1][2],dp[i-1][j-1][3],dp[i-1][j][4]})+a+b;
}
return 0&printf("%d",max({dp[n][k][0],dp[n][k][1],dp[n][k][2],dp[n][k][3],dp[n][k][4]}));
}
}
}
using namespace std;
int main(){
scanf("%d %d %d",&n,&m,&k);
return m==1?Subtask1::Solve():Subtask2::Solve();
}
9.「SNOI2017」英雄联盟(背包 dp)
$ $luogu
$ $首先说一下哈,这个里面的 $n \leq 10^6$,没这么麻烦。
$ $做 dp 题都需要简化题意,这道题的意思大概就是展示策略达到 $m$ 种的最小花费。
$ $我们有 $n$ 个英雄,每个英雄都是有一个皮肤的数量 $k_i$ 和花费 $c_i$ 的。很容易联想到我们的背包。这道题就是把每一个英雄看成一个分组,每组都有一个数量,花费固定。很经典的分组背包问题。我们定义 $dp_{i,j}$ 为买掉 $i$ 个皮肤用掉 $j$ Q 币的最大方案数。有 dp 方程:
$ $其中 $1 \leq p \leq k_i$。注意初始化 $dp_0=1$,因为什么都不买也算作一种方案。
$ $可以发现我们的二维数组死掉了。考虑优化空间。
$ $我们看到只需要考虑前 $i-1$ 维,可以考虑滚掉。也可以看到后面一维,实际上这就是一个类似于 01 背包的优化方法。直接暴力滚掉二维,倒序枚举当前的 Q 币数,然后正常背包。dp 式改进为:
$ $然后枚举花费 Q 币数,如果有 $m \leq dp_q$,输出 $q$。
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
long long n,m,dp[1000005],k[1000005],c[1000005],rest;
int main(){
scanf("%lld %lld",&n,&m);
for(long long i=1;i<=n;++i) scanf("%lld",&k[i]);
for(long long i=1;i<=n;++i) scanf("%lld",&c[i]),rest+=k[i]*c[i];
dp[0]=1;
for(long long i=1;i<=n;++i) for(long long j=rest;~j;--j) for(long long l=1;l<=k[i] && l*c[i]<=j;++l) dp[j]=max(dp[j],dp[j-l*c[i]]*l);
for(long long i=0;i<=rest;++i) if(dp[i]>=m) return printf("%lld",i)&0;
return 0;
}
10.「HAOI2015」树上染色(树形类背包 dp)
$ $luogu
$ $大概意思就是说,我们要在 $n$ 个节点中把 $k$ 个涂黑,然后计算两两黑节点和白节点的距离之和,求这个最大值?
$ $做过树形 dp 的人很容易想到 定义 $dp_{i,j}$ 为第 $i$ 个节点,并以 $i$ 为根在子树上选择 $j$ 个黑色节点的最大贡献。如果您是这么定义的,那么肯定 gg 了。
$ $为什么呢?因为我们不只有这颗子树,在这棵子树外,有更多的节点。
$ $所以说我们只能根据套路,发现我们定义 $dp_{i,j}$ 为以 $i$ 为根的子树选择 $j$ 个黑色节点的贡献。但是计算贡献是极慢的。所以说我们要考虑如何计算。
$ $考虑我们只有 $k$ 个黑色节点。在这里用了 $l$ 个,那么外面不就是 $k-l$ 个了么?
$ $所以说,我们在统计的时候,不以点去储存,而是用边去计算贡献。对于我们的 $dp$ 数组,贡献有:
$ $其中 $val$ 为当前边的权值,而 $size_i$ 为以 $i$ 为根的子树的大小。枚举 $l$。
$ $这实际上就变成了一个背包问题。考虑每一棵子树分配多少黑色节点,大概就是分配体积,算出贡献。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define mp make_pair
#define Edge pair<long long,long long>
using namespace std;
vector<Edge> G[2005];
long long dp[2005][2005],size[2005],n,k;
void DP(long long now,long long pre)
{
size[now]=1;
dp[now][0]=dp[now][1]=0;
for(unsigned long long i=0;i<G[now].size();++i)
{
long long to=G[now][i].first,val=G[now][i].second;
if(to==pre) continue;
DP(to,now);
size[now]+=size[to];
for(long long j=size[now];~j;--j) for(long long l=0;l<=min(j,size[to]);++l) if(dp[now][j-l]!=-1) dp[now][j]=max(dp[now][j],dp[now][j-l]+dp[to][l]+l*(k-l)*val+(size[to]-l)*(n-k+l-size[to])*val);
}
}
int main(){
memset(dp,-1,sizeof dp);
scanf("%lld %lld",&n,&k);
for(long long i=1;i<n;++i)
{
long long u,v,val;
scanf("%lld %lld %lld",&u,&v,&val);
G[u].push_back(mp(v,val));
G[v].push_back(mp(u,val));
}
DP(1,0);
printf("%lld",dp[1][k]);
return 0;
}
动态规划100题 11~20 题
$ $总集链接
11.「CF1101D」GCD Counting(思维树形 dp)
$ $luogu
$ $首先膜拜考场上面打点分治的巨佬 小ljs。
$ $观察题面,似乎没有什么可以直接下手的地方。但是观察数据范围,$a_i$ 这么小,肯定有蹊跷嘛。
$ $既然 $a_i \leq 2 \times 10^5$,所以 $a_i$ 的质因子应该极其之少,所以我们可以直接枚举质因子,大力 dp 就完了。
$ $考场上不应该在这道题上面花那么多时间的。。。当然 $a_i$ 如果大了,那就过不了了。。
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
//a_i 那么小,肯定有蹊跷
long long read()
{
long long x=0,f=1;
char c=getchar();
while(c<'0' || c>'9')
{
if(c=='-') f=-1;
c=getchar();
}
while(c>='0' && c<='9') x=(x<<1)+(x<<3)+(c^'0'),c=getchar();
return x*f;
}
vector<long long> prime[200005],appear[200005],G[200005];
long long n,a[200005],ans;
void dealWith(long long x,long long situ)
{
for(long long i=2;i*i<=x;++i)
{
if(x%i==0)
{
prime[situ].push_back(i);
appear[situ].push_back(1);
while(x%i==0) x/=i;
}
}
if(x>1) prime[situ].push_back(x),appear[situ].push_back(1);
}
void dfs(long long now,long long pre)
{
for(unsigned long long i=0;i<G[now].size();++i)
{
long long to=G[now][i];
if(to==pre) continue;
dfs(to,now);
for(unsigned long long j=0;j<prime[now].size();++j) for(unsigned long long k=0;k<prime[to].size();++k) if(prime[now][j]==prime[to][k]) ans=max(ans,appear[now][j]+appear[to][k]),appear[now][j]=max(appear[now][j],1+appear[to][k]);
}
if(a[now]>1) ans=max(ans,1ll);
}
int main(){
// freopen("count.in","r",stdin);
// freopen("count.out","w",stdout);
n=read();
bool flag=false;
for(long long i=1;i<=n;++i)
{
a[i]=read();
dealWith(a[i],i);
flag|=(a[i]>1);
}
if(!flag) return puts("0")&0;
for(long long i=1;i<n;++i)
{
long long u=read(),v=read();
G[u].push_back(v);
G[v].push_back(u);
}
dfs(1,0);
printf("%lld",ans);
while(1) return 0;
}
12.「JSOI2018」潜入行动(不简单的背包树形 dp)
$ $luogu
$ $初看题面:哦,这难道不是一道水题么?直接切嘛。
$ $类似于分类讨论被自控,被爸爸控制,被儿子控制嘛。
$ $再看题面,发现:如果在自己这里放上监控,是无法被控制的。于是我们的树形 dp 就宣告爆炸。
$ $因为根据讨论理性分析之后,我们发现,其实被控制是根本一样的。只有自己放或者不放的区别。
$ $考虑以上影响因素以及我们的经验,定义 $dp_{i,j,0 or 1,0 or 1}$ 表示以 $i$ 为根的子树用 $j$ 个监控器,(根可以不被监听,但是其它节点必须被监听)当前节点放不放监控器,根是否被监听,可以得到一个很长的 dp 方程,太长懒得打,就放在代码里面吧。
$ $但是这样就完了吗?这道题的难点就在于,我们这样的时间复杂度是 $O(nk^2)$ 的!!那么放上朴素代码。
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
//1
#define MOD 1000000007ll
using namespace std;
typedef long long LL;
/*
dp[i][j][0/1][0/1]:
以i为根,放j个监听器,根放了没有,被监听没有。
*/
vector<int> G[100005];
long long read()
{
long long x=0,f=1;
char c=getchar();
while(c<'0' || c>'9')
{
if(c=='-') f=-1;
c=getchar();
}
while(c>='0' && c<='9') x=(x<<1)+(x<<3)+(c^'0'),c=getchar();
return x*f;
}//2
int dp[100005][105][2][2],tmpdp[105][2][2],sizen[100005],n,k;
void DP(long long now,long long pre)
{
dp[now][0][0][0]=dp[now][1][1][0]=sizen[now]=1;
for(unsigned int i=0;i<G[now].size();++i)
{
int to=G[now][i];
if(to==pre) continue;
DP(to,now);
memset(tmpdp,0,sizeof tmpdp);
for(int j=0;j<=k;++j)
{
for(int l=0;l<=k-j;++l)//3
{
tmpdp[j+l][0][0]+=(
(LL)dp[now][j][0][0]*dp[to][l][0][1])%MOD,
tmpdp[j+l][0][0]%=MOD;
tmpdp[j+l][0][1]+=(((
(LL)dp[now][j][0][1]*dp[to][l][0][1])%MOD+
(LL)dp[now][j][0][1]*dp[to][l][1][1])+
(LL)dp[now][j][0][0]*dp[to][l][1][1])%MOD,
tmpdp[j+l][0][1]%=MOD;
tmpdp[j+l][1][0]+=((
(LL)dp[now][j][1][0]*dp[to][l][0][1])+
(LL)dp[now][j][1][0]*dp[to][l][0][0])%MOD,
tmpdp[j+l][1][0]%=MOD;
tmpdp[j+l][1][1]+=((((((
(LL)dp[now][j][1][1]*dp[to][l][0][0])%MOD+
(LL)dp[now][j][1][1]*dp[to][l][0][1])+
(LL)dp[now][j][1][1]*dp[to][l][1][0])%MOD+
(LL)dp[now][j][1][1]*dp[to][l][1][1])+
(LL)dp[now][j][1][0]*dp[to][l][1][0])+
(LL)dp[now][j][1][0]*dp[to][l][1][1])%MOD,
tmpdp[j+l][1][1]%=MOD;//dp方程
}
}
sizen[now]+=sizen[to];
memcpy(dp[now],tmpdp,sizeof tmpdp);
}
}
int main(){
// freopen("sneak.in","r",stdin);
// freopen("sneak.out","w",stdout);
n=read(),k=read();
for(int i=1;i<n;++i)
{
int u=read(),v=read();
G[u].push_back(v);
G[v].push_back(u);
}
DP(1,0);
printf("%lld",(dp[1][k][0][1]+dp[1][k][1][1])%MOD);
while(1) return 0;
}
$ $于是我们只能考虑优化。首先来试一下优化常数吧。
$ $优化 1(对应注释1):你的八聚氧。
$ $优化 2(对应注释2):你的 fread()。
$ $优化 3(对应注释3):放不了这么多放什么放,把 j<=k 改成 min(k,sizen[now]),l<=k-j 改成 min(k-j,sizen[to])。
$ $交一发,为什么 A 了??
$ $删去优化 1 和 2,发现其实 1 和 2 并没有起很大作用,删掉 3 就只有 30 分了。这是为什么呢?
$ $首先分析一下复杂度,这个优化看似是一个常数优化,但是实际上起到了至关重要的作用。
$ $考虑证明,思来想去也不过三种情况:
一个节点有两个儿子形成的子树大小大于 $k$:实际上合并次数就不会超过 $O(\frac{n}{k})$ 了。这样之后就会变成 $O(k)$。实际上这应该是最快的一种情况。
一个节点有一个儿子形成的子树大小小于 $k$,合并了就成了大于 $k$ 了:因为子树的所有节点都经过一次背包合并,实际上均摊之后也只有 $O(k)$ 了。
otherwise:显然这个东西是不足 $O(k)$ 的。每次加入一个点,不足 $k$ 个节点,那么对于某一个特定的点,它的贡献实际上是每次加入的子树大小,还没有 $O(k)$ 了。
$ $综上所述:我们的时间复杂度为 $O(nk)$。
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#define MOD 1000000007ll
using namespace std;
typedef long long LL;
/*
dp[i][j][0/1][0/1]:
以i为根,放j个监听器,根放了没有,被监听没有。
*/
vector<int> G[100005];
long long read()
{
long long x=0,f=1;
char c=getchar();
while(c<'0' || c>'9')
{
if(c=='-') f=-1;
c=getchar();
}
while(c>='0' && c<='9') x=(x<<1)+(x<<3)+(c^'0'),c=getchar();
return x*f;
}
int dp[100005][105][2][2],tmpdp[105][2][2],sizen[100005],n,k;
void DP(long long now,long long pre)
{
dp[now][0][0][0]=dp[now][1][1][0]=sizen[now]=1;
for(unsigned int i=0;i<G[now].size();++i)
{
int to=G[now][i];
if(to==pre) continue;
DP(to,now);
memset(tmpdp,0,sizeof tmpdp);
for(int j=0;j<=min(k,sizen[now]);++j)
{
for(int l=0;l<=min(k-j,sizen[to]);++l)
{
tmpdp[j+l][0][0]+=(
(LL)dp[now][j][0][0]*dp[to][l][0][1])%MOD,
tmpdp[j+l][0][0]%=MOD;
tmpdp[j+l][0][1]+=(((
(LL)dp[now][j][0][1]*dp[to][l][0][1])%MOD+
(LL)dp[now][j][0][1]*dp[to][l][1][1])+
(LL)dp[now][j][0][0]*dp[to][l][1][1])%MOD,
tmpdp[j+l][0][1]%=MOD;
tmpdp[j+l][1][0]+=((
(LL)dp[now][j][1][0]*dp[to][l][0][1])+
(LL)dp[now][j][1][0]*dp[to][l][0][0])%MOD,
tmpdp[j+l][1][0]%=MOD;
tmpdp[j+l][1][1]+=((((((
(LL)dp[now][j][1][1]*dp[to][l][0][0])%MOD+
(LL)dp[now][j][1][1]*dp[to][l][0][1])+
(LL)dp[now][j][1][1]*dp[to][l][1][0])%MOD+
(LL)dp[now][j][1][1]*dp[to][l][1][1])+
(LL)dp[now][j][1][0]*dp[to][l][1][0])+
(LL)dp[now][j][1][0]*dp[to][l][1][1])%MOD,
tmpdp[j+l][1][1]%=MOD;
}
}
sizen[now]+=sizen[to];
memcpy(dp[now],tmpdp,sizeof tmpdp);
}
}
int main(){
// freopen("sneak.in","r",stdin);
// freopen("sneak.out","w",stdout);
n=read(),k=read();
for(int i=1;i<n;++i)
{
int u=read(),v=read();
G[u].push_back(v);
G[v].push_back(u);
}
DP(1,0);
printf("%lld",(dp[1][k][0][1]+dp[1][k][1][1])%MOD);
while(1) return 0;
}
13.「CF1114D」Flood Fill(套路区间 dp)
$ $luogu
$ $实际上这是个模板。考虑枚举长度和长度区间,区间枚举划分点,这实际上是 $O(n^3)$ 的。只能优化区间划分点。每次加入的话,其实是不需要枚举划分点的。把序列 unique 掉,每次加入就不会有相同的影响了。
#include<bits/stdc++.h>
using namespace std;
int n,dp[5005][5005],a[5005],len;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
len=unique(a+1,a+1+n)-a-1;
for(int i=1;i<=len;++i)
{
for(int l=1,r=i+1;r<=len;++l,++r)
{
if(a[l]==a[r]) dp[l][r]=dp[l+1][r-1]+1;
else dp[l][r]=min(dp[l+1][r],dp[l][r-1])+1;
}
}
printf("%d",dp[1][len]);
return 0;
}
14.「CF149D」Coloring Brackets(限制性区间 dp)
$ $luogu
$ $其实也是裸题,只不过加上了一些预处理和颜色限制。我们首先考虑计算括号对应,很容易打出这样的代码。
for(long long i=1;i<=n;++i)
{
if(bracket[i]=='(') S.push(i);
else dy[S.top()]=i,S.pop();
}
$ $加上颜色限制,定义 $dp_{i,j,0 or 1 or 2,0 or 1 or 2}$ 为区间 $[i,j]$,$i$ 不染/染成红色/染成蓝色,$j$ 同理的方案数,递归长序列,dp 合并小序列:
如果 $l+1=r$ ,因为这是一个合法的括号序列,包含下面的操作话这一定是一对括号;
如果 $dy_l=r$,递归处理 $l+1,r-1$,合并组成 dp;
其他情况是最麻烦的,这是两个或以上的括号序列组成的,分别划分,依次 dp,合并即可。
$ $详见代码。
#include<cstdio>
#include<algorithm>
#include<queue>
#include<iostream>
#include<cstring>
#include<stack>
#define MOD 1000000007ll
using namespace std;
stack<long long> S;
long long dp[705][705][3][3],dy[705],n;
char bracket[705];
/*
dp[l][r][0/1/2][0/1/2];
[l,r] l=0/1/2 r=0/1/2
还是写记忆化好理解。xd
*/
void dfs(long long l,long long r)
{
if(l+1==r)
{
dp[l][r][0][1]=dp[l][r][0][2]=dp[l][r][1][0]=dp[l][r][2][0]=1;
return ;
}
if(dy[l]==r)
{
dfs(l+1,r-1);
for(long long i=0;i<=2;++i)
{
for(long long j=0;j<=2;++j)
{
if(i!=1) dp[l][r][1][0]+=dp[l+1][r-1][i][j],dp[l][r][1][0]%=MOD;
if(i!=2) dp[l][r][2][0]+=dp[l+1][r-1][i][j],dp[l][r][2][0]%=MOD;
if(j!=1) dp[l][r][0][1]+=dp[l+1][r-1][i][j],dp[l][r][0][1]%=MOD;
if(j!=2) dp[l][r][0][2]+=dp[l+1][r-1][i][j],dp[l][r][0][2]%=MOD;
}
}
}
else
{
dfs(l,dy[l]);
dfs(dy[l]+1,r);
for(long long i=0;i<=2;++i) for(long long j=0;j<=2;++j) for(long long k=0;k<=2;++k) for(long long m=0;m<=2;++m) if(!(j && j==k)) dp[l][r][i][m]+=dp[l][dy[l]][i][j]*dp[dy[l]+1][r][k][m]%MOD,dp[l][r][i][m]%=MOD;
}
}
int main(){
// freopen("coloring.in","r",stdin);
// freopen("coloring.out","w",stdout);
scanf("%s",bracket+1);
n=strlen(bracket+1);
for(long long i=1;i<=n;++i)
{
if(bracket[i]=='(') S.push(i);
else dy[S.top()]=i,S.pop();
}
dfs(1,n);
long long ans=0;
for(long long i=0;i<=2;++i) for(long long j=0;j<=2;++j) ans+=dp[1][n][i][j],ans%=MOD;
printf("%lld",ans);
return 0;
}
15.「CQOI2009」叶子的染色(猜结论+树形 dp)
$ $luogu
$ $真的没想到 T3 是最简单的。。。
$ $首先猜个结论:怎么选根答案都是一样的。(毕竟这是猜结论,我也不知道为什么)。
$ $然后再一个结论:我们把叶子染色,实际上就是把根染色。因为叶子染色只跟上面的颜色有关。
$ $然后就完了??定义 $dp_{i,0 or 1}$ 为 $i$ 为根,$i$ 染成黑色还是白色。则有 dp 方程:
$ $然后真的就完了。注意排斥掉和叶子颜色不同的方案。
#include<cstdio>
#include<algorithm>
#include<queue>
#include<iostream>
#include<cstring>
using namespace std;
vector<int> G[100005];
bool color[100005];
int dp[100005][2],m,n;
/*
dp[root][0/1]:root 为根 染成什么 最少多少个。
*/
void dfs(int now,int pre)
{
if(now<=n)
{
dp[now][color[now]]=1;
dp[now][!color[now]]=2147483647;
return ;
}
dp[now][1]=dp[now][0]=1;
for(unsigned int i=0;i<G[now].size();++i)
{
int to=G[now][i];
if(to==pre) continue;
dfs(to,now);
dp[now][0]+=min(dp[to][1],dp[to][0]-1);
dp[now][1]+=min(dp[to][1]-1,dp[to][0]);
}
}
int main(){
freopen("leave.in","r",stdin);
freopen("leave.out","w",stdout);
scanf("%d %d",&m,&n);
for(int i=1,tmp;i<=n;++i) scanf("%d",&tmp),color[i]=bool(tmp);
for(int i=1;i<m;++i)
{
int u,v;
scanf("%d %d",&u,&v);
G[u].push_back(v);
G[v].push_back(u);
}
dfs(n+1,-1);
printf("%d",min(dp[n+1][0],dp[n+1][1]));
return 0;
}
16.「HAOI2016」字符合并(区间 dp x 状压 dp)
$ $luogu
$ $根据经验,$k$ 很小,并且只有 01 串,很容易想到状压 dp。
$ $因为分数非负,考虑把能合的全部都合起来。我们考虑合并完成后展开,各个区间一定是不相交的。考虑用上区间 dp。
$ $区间 dp 套路,枚举中间端点。合并成一位 0 或 1 一定会弄掉 $k$ 个字符变成 1 个(因为其中区间不相交),所以直接 ptt+=k-1 就好。
$ $然后特殊情况是区间长度刚好是 $k$。那么直接合并,用两个临时变量储存。(因为修改之后能够修改其他的值,不好操作)。
$ $最后说一下状态定义:定义 $dp_{i,j,S}$ 为合并 $[i,j]$ 区间,状态为 $S$。有 dp 方程:
$ $最后注意下枚举顺序,考虑用到 $dp_{i,ptt-1}$ 和 $dp_{ptt,j}$,枚举区间一定要倒序枚举。
$ $答案为 $\max \{ dp_{1,n}\}$
#include<cstdio>
#include<queue>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<set>
#include<map>
#define lc(x) x<<1ll
#define rc(x) x<<1ll|1ll
using namespace std;
char t[3005];
int n,m;
long long NegaInf,a[3005],cnt[2600],val[2600],dp[305][305][305];
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i) scanf("%lld",&a[i]);
for(int i=0;i<=(1<<m)-1;++i) scanf("%lld %lld",&cnt[i],&val[i]);
memset(dp,128,sizeof dp);
for(int i=1;i<=n;++i) dp[i][i][a[i]]=0;
NegaInf=dp[0][0][0];
for(int dis=2;dis<=n;++dis)
{
for(int i=1,j=dis;j<=n;++i,++j)
{
long long lena=(j-i)%(m-1);
lena=!lena?m-1:lena;
for(int ptt=j;ptt>=i+1;ptt-=m-1)
{
for(int k=0;k<=(1<<lena)-1;++k)
{
if(dp[i][ptt-1][k]==NegaInf) continue;
if(dp[ptt][j][0]!=NegaInf) dp[i][j][lc(k)]=max(dp[i][j][lc(k)],dp[i][ptt-1][k]+dp[ptt][j][0]);
if(dp[ptt][j][1]!=NegaInf) dp[i][j][rc(k)]=max(dp[i][j][rc(k)],dp[i][ptt-1][k]+dp[ptt][j][1]);
}
}
if(lena==m-1)
{
long long rear0=NegaInf,rear1=NegaInf;
for(int k=0;k<=(1<<m)-1;++k)
{
if(dp[i][j][k]!=NegaInf)
{
if(cnt[k]) rear1=max(rear1,dp[i][j][k]+val[k]);
else rear0=max(rear0,dp[i][j][k]+val[k]);
}
}
dp[i][j][0]=rear0,dp[i][j][1]=rear1;
}
}
}
long long ans=NegaInf;
for(int i=0;i<=(1<<m)-1;++i) ans=max(ans,dp[1][n][i]);
printf("%lld",ans);
return 0;
}
17.「GXOI/GZOI2019」宝牌一大堆(我也不知道是什么 dp)
$ $luogu
$ $作为一个玩雀魂的想做一下麻将题,发现 ZJOI 的麻将题过于毒瘤,这个反而比较简单。
$ $考虑到只有刻子/顺子/杠子/雀头,面子与雀头只跟当前牌,下一张牌,下下张牌有关系,其他需要注意的有组成了多少个面子,有没有雀头。考虑到将这五个东西联合当前牌是什么塞进 dp 中。但是我们很快发现在这个模式下杠了牌就是杠精,原因是 $C_4^3=4C_4^4$。即使这张牌是 dora 也无济于事,没有用。(杠杠杠,杠出新天地,杠出宝牌一大堆)
$ $现在考虑到这六维的信息。定义 $dp_{i,,j1 or 0,k,l,o}$ 为在第 $i$ 张牌(共有 34 张牌),组成的牌中有没有雀头,组成了 $j$ 个面子,$i$ 张牌用了 $k$ 张,第 $i+1$ 张牌用了 $l$ 张,$i+2$ 用了 $o$ 张,分有无雀头两边 dp,分情况讨论新组成顺子,新组成刻子,新组成雀头就OK了。
$ $定义 $dp_{i,j,0 or 1 ,k,l,o}$ 为选到 $i$ 张牌,组成 $j$ 刻子,有无雀头,$i$ 张牌用了 $k$ 张,$i+1$ 用了 $l$ 张,$i+2$ 用了 $o$ 张。对有无雀头分别 dp,考虑新增雀头/刻子/顺子讨论即可。
$ $超时了,考虑优化:
$l \leq 2,o \leq 2$。这是因为当 $l>2$ 时,它是一个刻子,更别说 $l>2,o>2$ 了,这直接是一个三连刻好吗?(你听说过三连刻没有.jpg,古役,两番?);(优化 1)
组合数打表计算,不要直接计算;(优化 2)
如果当前 dp 值为 0,直接
continue,这是因为你之前组成的牌胡不了。。(优化 3)
$ $七对子贪心选择贡献最大的七个对子,国士无双(三大民工役满之一,剩下为大三元和四暗刻)枚举哪一张用两次,$O(169)$ 枚举就 OK。
$ $看不懂就领略一下精神就好了。。。
#include<cstdio>
#include<algorithm>
#include<queue>
#include<iostream>
#include<cstring>
#define mahjongMaxn 35
using namespace std;
const int initC[7][7]=
{
{1,0,0,0,0},
{1,1,0,0,0},
{1,2,1,0,0},
{1,3,3,1,0},
{1,4,6,4,1}
};//一定要做的事
void write(long long t)
{
if(t<0) putchar('-'),t=-t;
if(t>9) write(t/10);
putchar('0'+t%10);
}
const int Kin[]={0,1,9,10,18,19,27,28,29,30,31,32,33,34};//国士无双需要的牌,Kokushimusou in need
const bool shien[]={0,1,1,1,1,1,1,1,0,0,1,1,1,1,1,1,1,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0};//能做顺子开头的牌
int rest[mahjongMaxn+5],isDora[mahjongMaxn+5];//剩下多少张以及是否是 dora
long long dp[mahjongMaxn+5][6][4][6][4][4];
int C(int x,int y){return initC[x][y];}//可以换成正常计算(优化 2)
int mahjong(char x)
{
switch (x)
{
case 'E': return 28;
case 'S': return 29;
case 'W': return 30;
case 'N': return 31;
case 'Z': return 32;
case 'B': return 33;
case 'F': return 34;
}
return 10086001;
}
int mahjong(char x,char y)
{
switch (y)
{
case 'm': return x-'0';
case 'p': return 9+x-'0';
case 's': return 18+x-'0';
}
return 10086001;
}//输入,返回麻将标号
long long Kokushimusou()
{
for(int i=1;i<=13;++i) if(!rest[Kin[i]]) return 0;
long long ans=0;
for(int i=1;i<=13;++i)
{
long long tmp=C(rest[Kin[i]],2)*isDora[Kin[i]]*isDora[Kin[i]]*13;
for(int j=1;j<=13;++j) if(i!=j) tmp*=isDora[Kin[j]]*rest[Kin[j]];
ans=max(ans,tmp);
}
return ans;
}//国士无双
long long Chitoicu()
{
long long ans=7;
priority_queue<long long> PQ;
for(int i=1;i<=mahjongMaxn-1;++i) PQ.push(isDora[i]*isDora[i]*C(rest[i],2));
if(PQ.size()<7) return 0;
for(int i=1;i<=7;++i) ans*=PQ.top(),PQ.pop();
return ans;
}//七对子
long long OthersDP(){
long long ans=0;
dp[1][0][0][0][0][0]=1;
for(int i=1;i<=mahjongMaxn-1;++i)
{
for(int j=0;j<=4;++j)
{
for(int k=0;k<=4;++k)
{
for(int l=0;l<=2;++l)
{
for(int o=0;o<=2;++o)//(优化 1)
{
long long kc1=dp[i][j][0][k][l][o],kc2=dp[i][j][1][k][l][o];
if(!kc1 && !kc2) continue;//(优化 3)
if(rest[i]-k>=2) dp[i][j][1][k+2][l][o]=max(dp[i][j][1][k+2][l][o],kc1/C(rest[i],k)*C(rest[i],k+2)*isDora[i]*isDora[i]);//新雀头
if(j<4)
{
if(rest[i]-k>=3)
dp[i][j+1][0][k+3][l][o]=
max(dp[i][j+1][0][k+3][l][o],
kc1/C(rest[i],k)*C(rest[i],k+3)*isDora[i]*isDora[i]*isDora[i]),
dp[i][j+1][1][k+3][l][o]=
max(dp[i][j+1][1][k+3][l][o],
kc2/C(rest[i],k)*C(rest[i],k+3)*isDora[i]*isDora[i]*isDora[i]);//新刻子
if(shien[i] && rest[i]>k && rest[i+1]>l && rest[i+2]>o && l!=2 && o!=2)
dp[i][j+1][0][k+1][l+1][o+1]=max(dp[i][j+1][0][k+1][l+1][o+1],
kc1
/C(rest[i],k)*C(rest[i],k+1)*isDora[i]
/C(rest[i+1],l)*C(rest[i+1],l+1)*isDora[i+1]
/C(rest[i+2],o)*C(rest[i+2],o+1)*isDora[i+2]),
dp[i][j+1][1][k+1][l+1][o+1]=max(dp[i][j+1][1][k+1][l+1][o+1],
kc2
/C(rest[i],k)*C(rest[i],k+1)*isDora[i]
/C(rest[i+1],l)*C(rest[i+1],l+1)*isDora[i+1]
/C(rest[i+2],o)*C(rest[i+2],o+1)*isDora[i+2]);//新顺子
}
dp[i+1][j][0][l][o][0]=max(dp[i+1][j][0][l][o][0],kc1);
dp[i+1][j][1][l][o][0]=max(dp[i+1][j][1][l][o][0],kc2);//自身状态继承下一状态
if(j==4) ans=max(ans,kc2);//四个刻子和一个雀头就以经胡牌,保存答案
}
}
}
}
}
return ans;
}
void Prepare()
{
fill(rest,rest+mahjongMaxn,4);
fill(isDora,isDora+mahjongMaxn,1);
memset(dp,0,sizeof dp);
}
void ReadMahjongRiver()
{
char s[2];
while(scanf("%s",s))
{
if(s[0]=='0') return ;
if(s[1]=='\0') --rest[mahjong(s[0])];
else --rest[mahjong(s[0],s[1])];
}
}
void ReadDora()
{
char s[2];
while(scanf("%s",s))
{
if(s[0]=='0') return ;
if(s[1]=='\0') isDora[mahjong(s[0])]=2;
else isDora[mahjong(s[0],s[1])]=2;
}
}//Input
int main(){
long long T;
scanf("%lld",&T);
while(T-->0)
{
Prepare();
ReadMahjongRiver();
ReadDora();
write(max({Chitoicu(),Kokushimusou(),OthersDP()}));//C++11标准
puts("");
}
return 0;
}
18.「UVA1452」Jump(约瑟夫问题变形)
$ $luogu
$ $注:以上皆为 0 开头,代表队伍中的 1,$n-1$ 代表第 $n$ 人。
$ $这实际上是一个约瑟夫问题的一个变形。首先回到约瑟夫问题,它的实质是:将 $n$ 个人的子问题化成 $n-1$ 个,在同时建立一个映射关系,也就是我们的递推数组。我们要求最后一个人,就要倒退回去推出 $n$ 个人的情况。得到了最后一个人是谁,在倒推倒数第二人,倒数第三人即可。
$ $所以我们定义 $dp_i$ 为 $i-1$ 个人出列后,接下来应该让谁出列(同时调整队列顺序与编号)。我们最后一个出列的人因为在队头,所以编号一定为 0。因此 $dp_1=0$。题目定义得出递推方程:
$ $即:
$ $考虑到我们要求倒数三个人,所以分别令 $dp_1=0,dp_1=1,dp_2=2$ 就可以分别求出倒数第一个,倒数第二个和第三个了。
$ $这里就直接把数组滚了,代码会有点奇怪。因为 0 是开头,所以答案注意加 1。
$ $滚了数组之后代码可能有点怪,可以自行理解一下。
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
int main(){
int T;
scanf("%d",&T);
while(T-->0)
{
int n,k;
scanf("%d %d",&n,&k);
int a=0,b=(k-1)%2,c=(k-1)%3;
for(int i=2;i<=n;++i) a+=k,a%=i;
for(int i=3;i<=n;++i) b+=k,b%=i;
for(int i=4;i<=n;++i) c+=k,c%=i;
printf("%d %d %d\n",c+1,b+1,a+1);
}
return 0;
}
19.「CF235B」Let’s play OSU! 和 「BZOJ4318」OSU!(期望 dp)
$ $因为前者是后者的简化版,所以放一起了,我多良心啊。
$ $因为 $(x+1)^2=x^2+2x+1$,而 $E(x+y)=E(x)+E(y)$,我们设 $osu$ 为线性期望(类似于一次),$dp$ 表示答案。很容易得到:
$ $综上,答案为 $dp_n$。
#include<cstdio>
#include<algorithm>
using namespace std;
double osu[100005],dp[100005];
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
double cure;
scanf("%lf",&cure);
osu[i]=cure*(osu[i-1]+1);
dp[i]=dp[i-1]+cure*(2*osu[i-1]+1);
}
printf("%.10f",dp[n]);
return 0;
}
$ $然后看到加强版。
$ $因为 $(x+1)^3=x^3+3x^2+3x+1$。
$ $考虑到 $E(x)$ 中的 $x$ 增加 1,答案就多了 $E(3x^2+3x+1)$。又去考虑 $(x+1)^2$,同理可得。线性的比较简单,不再概述。
$ $返回到题目,用 $osu1$ 维护 $x$ 的期望,$osu2$ 维护 $x^2$ 的期望,$dp$ 维护答案,也就是 $x^3$ 的期望,有:
$ $综上,答案为 $dp_n$。
#include<cstdio>
#include<algorithm>
using namespace std;
double osu1[100005],osu2[100005],dp[100005];
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
double cure;
scanf("%lf",&cure);
osu1[i]=(osu1[i-1]+1)*cure;
osu2[i]=(osu2[i-1]+2*osu1[i-1]+1)*cure;
dp[i]=dp[i-1]+(3*osu2[i-1]+3*osu1[i-1]+1)*cure;
}
printf("%.1f",dp[n]);
return 0;
}
$ $至于为什么变量名叫 cure,是因为玩 OSU 需要解药。
$ $我怎么就管不住我这手呢???
20.「CF76F」Tourist(LIS 变形)
$ $luogu
$ $不得不说是一道好题。
$ $考虑到我们将每一个事件按时间排序之后,可以很容易的得到 dp 式。我们从一个点走到另外一个点,dp 值加 1 即可。
$ $一个点走到另一个点的条件是:$|x_i-x_j| \leq |t_i-t_j| \times v$。从这里怎么下手?
$ $首先说结论,$-x_i+t_i \times v \leq -x_i+t_j \times v \operatorname{and} x_i+t_i \times v \leq x_j+t_j \times v$ 和上面那个式子等价。
$ $假设 $t_i \leq t_j$,当 $x_i \geq x_j$ 时,$x_i -x_j \leq (t_j -t_i) \times v$ ,否则 $x_j-x_i \leq (t_j-t_i)\times v$。
$ $去掉前提。我们假设 $a_i=x_i + t_i \times v,b_i=x_i+t_j \times v$。如果一个点走到另一个点的话,必有 $a_i \leq a_j,b_i \leq b_j$。
$ $这里没看懂可以在理解一下,是挺麻烦的。
$ $现在我们得出 $a_i,b_i$ 单调。按 $a_i,b_i$ 排个序,求最长不下降子序列就行了。特殊的,对于第一个问题,我们只需要 $a_i,b_i \geq 0$ 的点就行了。
#include<cstdio>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#include<iostream>
#include<cstring>
using namespace std;
int x[100005],t[100005],n,v;
struct Point{//Map to an event.
int x,y;
bool operator < (Point q) const
{
if(x!=q.x) return x<q.x;
return y<q.y;
}
Point() {}
Point(int X,int Y){x=X,y=Y;}
}event[100005];
int main(){
cin>>n;
for(int i=1;i<=n;++i) cin>>x[i]>>t[i];
cin>>v;
int tot=0;
for(int i=1;i<=n;++i) if(v*t[i]+x[i]>=0 && v*t[i]-x[i]>=0) event[++tot]=Point(v*t[i]+x[i],v*t[i]-x[i]);
sort(event+1,event+1+tot);
multiset<int> S;
multiset<int>::iterator Sit;
for(int i=1;i<=tot;++i)
{
Sit=S.upper_bound(event[i].y);
if(Sit!=S.end()) S.erase(Sit);
S.insert(event[i].y);
}
cout<<S.size()<<' ';
S.clear();
for(int i=1;i<=n;++i) event[i]=Point(v*t[i]+x[i],v*t[i]-x[i]);
sort(event+1,event+1+n);
for(int i=1;i<=n;++i)
{
Sit=S.upper_bound(event[i].y);
if(Sit!=S.end()) S.erase(Sit);
S.insert(event[i].y);
}
cout<<S.size()<<endl;
return 0;
}
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1275881998@qq.com
文章标题:DP 100题
本文作者:Forgotten
发布时间:2020-02-11, 13:25:00
最后更新:2020-02-11, 13:22:22
原始链接:http://forgotten-myself.github.io/2020/02/11/DP100%E9%A2%98/版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。